In "Clocks, Chords, and Roots of Unity: A Love Song to Mathematics," Dr. Juliana Bukoski ties together the mathematics behind how we tell time, music, and Roots of Unity (which were a focus of her thesis work while a graduate student at the UNL Department of Mathematics). What mathematical idea ties all three concepts together? Something called modular arithmetic.
So what is modular arithmetic? Let’s illustrate this via an example. Normally, if I ask you “what’s 10+13?” you’d answer 23. Basic addition, right? But if we’re trying to tell time, we may reframe this question as “The time is 10 o'clock. What will be the time 13 hours from now?” The answer should be 11 o’clock, but how do we calculate that? Well, we use modular arithmetic. Modular arithmetic works similarly to regular arithmetic except that numbers “wrap around” when they reach a certain value, called the “modulus”. Counting “modulo 12” “mod 12” works similarly to basic math, we just start over after counting up to 12 (“…, 10, 11, 12, 1, 2, 3,…). So (10+13) mod 12 = 11.
Note: Telling time using a 12-hour clock provides a real-world representation of the integers modulo 12, a set of 12 distinct elements. The elements of this set are typically expressed as {0,1,2,3,4,5,6,7,8,9,10,11} – so instead of using “12” as an element we normally use “0”.
Something to think about with students: What if I asked you: “The time is 11:45. What time is it 30 minutes from now?” How does modular arithmetic help students calculate time in this scenario?
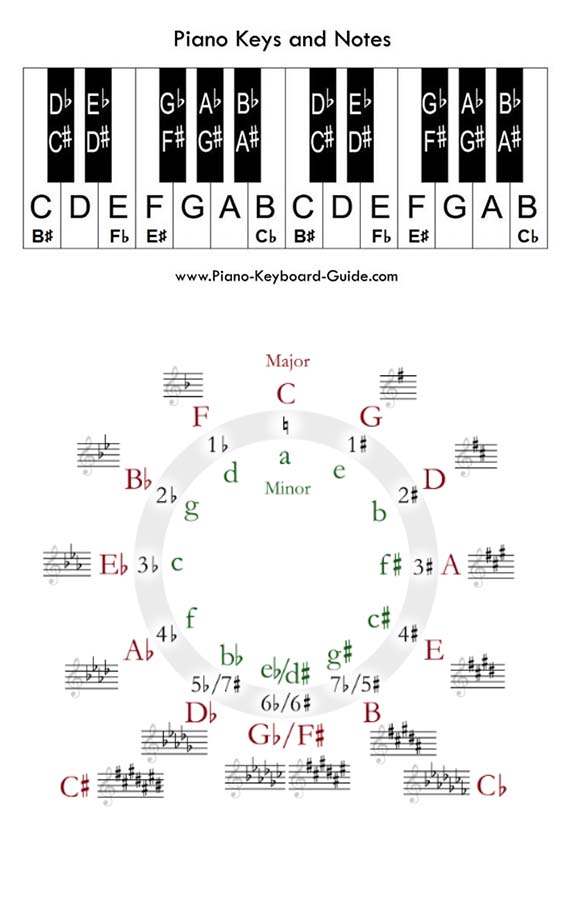
Modular arithmetic is one of the first examples we encounter of addition working differently from what we expect, and it appears in various forms in real life. Another example is in music. If you’ve ever looked at a piano keyboard, you’ll notice how the keys have a repeating pattern to them: groups of 12 keys: seven white keys and five black keys (starting at the key labeled “C”). These form an “octave”. Each octave has 12 pitches (a C pitch, a D pitch, etc.). The set of all C pitches from all octaves is the C “pitch class”.
See figure at right of piano keys.
In Juliana’s song she hits all 12 pitch classes. She represents these 12 pitch classes on a clock (to emphasize the connection with the 12 hour places on a clock). You may be wondering why she represented these pitch classes in this order. As it turns out, this image represents something called the “Circle of Fifths,” which is useful in helping musicians read music. It has to do with the number of flat and sharp pitches in a major scale, but we’ll leave those details to the reader!
See figure at right of two octaves.
Now that your students have that background, they can watch and listen to the song (and a brief introduction from Juliana) here: https://youtu.be/ViaUJBW-2IA