A cooking recipe provides a detailed list of ingredients and instructions that allow a delicious dish to be repeatedly recreated by others. Fellow chefs who strictly follow a recipe should, in theory, be able to duplicate the same dish. Of course, one random ingredient can cause surprising results in the kitchen.
Like recipes, computational algorithms can also be duplicated and should, in theory, produce the same results, but a random ingredient can present scientists with unexpected outcomes and other problems.
With a new grant from the National Science Foundation and in collaboration with faculty at Iowa State University, School of Computing Professor Vinodchandran Variyam will launch the “New Directions in Algorithmic Replicability” project, which will address the challenge of randomness in computational processes to ensure the reproducibility and replicability of algorithms.
According to Variyam, reproducibility is a cornerstone of scientific methodology and states that research practices should be repeatable and yield consistent results regardless of who performs the research. However, the inherent randomness that occurs within algorithms poses a direct contradiction to that principle.
“In computation, randomness is a very required ingredient,” Variyam said. “Whether it's for predicting the weather or simulating cosmic phenomena, randomness is integral for modeling complex systems, but it complicates the pursuit of reproducibility.”
This issue has raised critical concerns in various scientific disciplines, especially in recent years as the use of data-driven research continues to increase. Since randomness is virtually impossible to eliminate, Variyam’s project instead aims to restrict its effects.
“The initiative is designed to ensure predictable outcomes from computations, even in the face of inherent unpredictability, by adopting an innovative approach that intersects computation with geometry,” Variyam said. “We found that a certain type of replicability has a strong connection to geometry, and so in certain settings, it boils down to solving a geometry problem.
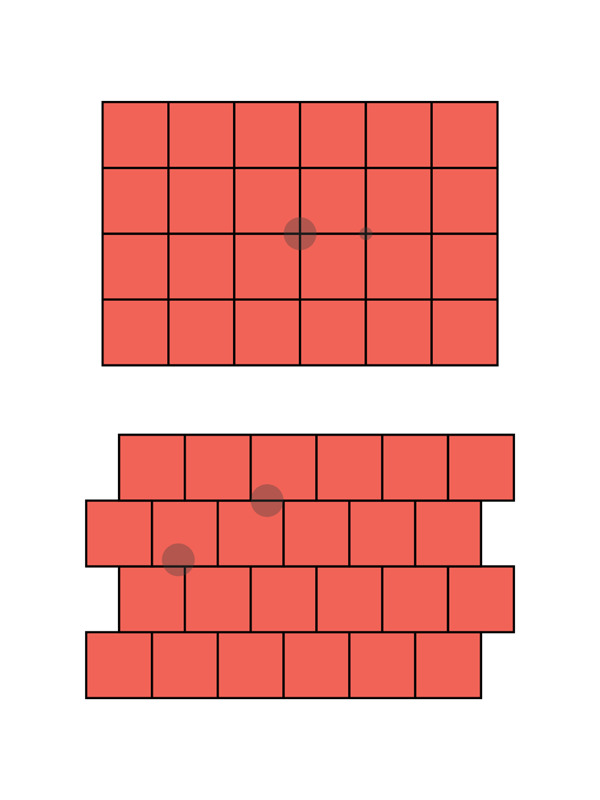
Variyam’s project will explore randomized algorithms through the concept of geometric partitioning. The project’s innovative use of “secluded partitions” can be visualized as placing a small circle on a grid. Regardless of where the circle is placed on the grid, it touches only a few squares. In computational spaces, the secluded partitions limit overlap and ensure “controlled randomness,” or the idea that any randomness that occurs can only influence a few predictable sets of outcomes.
“The introduction of secluded partitions not only facilitates algorithmic replicability, but it also paves the way for new theoretical frameworks and tools,” Variyam said. “These innovations have the potential to revolutionize our understanding of multidimensional spaces and address perennial challenges across mathematics, physics, and related disciplines. The partitions we designed in fact already found applications in quantum computing.”
The project and its possibilities have quickly garnered recognition within the academic community. Key contributions to the project have already been published in premier computer science venues, including the Symposium on Theory of Computing (STOC) and the Conference on Neural Information Processing Systems (NeurIPS).
Variyam said the widespread interest and acknowledgement is a testament to the future positive impact the project will undoubtedly have on many sectors of science.
“It’s exciting that we’re developing foundations for these practically significant issues for the first time, not only for computing but for these mathematical concepts that come into play.”
Photo description: Figure 1 shows standard grid partitions in two dimensions with poor seclusion parameters. Any small circle intersects four squares. Figure 2 shows the optimal secluded partitions. Any small circle only intersects three squares. The challenge is to design higher dimensional partitions with optimal seclusion parameters.